データの活用	２３　玉　(確率)　３	月　　　日（　　）
以下の問題では,どの玉が取り出されることも同様に確からしいものとします。

１	徳島県立高校　（Ｒ５年）　★★	５	法政大国際高校　（Ｒ４年）　★★
赤玉3個,白玉2個,青玉1個がはいっている箱から,同時に2個の玉を取り出すとき,取り出した2個の玉の色が異なる確率を求めなさい。		白球3個,赤球2個,青球1個を1つの袋に入れる。その袋の中から3個の球を無作為に同時に取り出すとき,取り出した3個の中に白球が2個だけ入っている確率を求めよ。
２	山梨県立高校　（Ｒ６年）　★★★	６	土浦日本大高校　（Ｒ５年）　★★
箱の中に,赤球2個,青球1個,白球2個が入っている。この箱の中から球を同時に2個取り出たとき,取り出した球の中に青球が含まれる確率を求めなさい． 2/5		袋の中に�@,�A,�Bと書かれた玉が1つずつ入っている。この袋から無作為に1つの玉を取り出し,数字を記録して袋の中に戻す操作を3回行う。 　記録された数字を左から順に並べて3桁の整数を作るとき,奇数となる確率は(　　)であり,4の倍数となる確率は(　　)である。
３	お茶の水女子大附属高校　（Ｒ４年）　★★★	７	栃木県立高校　（Ｒ６年）　★★★
袋の中に,赤玉,白玉,青玉の3色の玉が入っている。3色の玉の個数の比は,この順に2:3:4である。総数はわかっていない。 (1) この袋から1つだけ玉を取り出すとき,白玉である確率を求めなさい。 (2) 玉を取り出す前に,この袋から,青玉を2個減らし,赤玉を6個と白玉をm個加えた後,袋から1つだけ玉を取り出したとき,どの色の玉も取り出される確率は等しくになるという。mの値を求めなさい。		袋の中に,1から5までの数字が1つずつ書かれた5個の玉が入っている。 (1) Aさんが玉を1個取り出し,取り出した玉を袋の中に戻さずに,続けてBさんが玉を1個取り出す。2人の玉の取り出し方は全部で何通りか。 (2) Aさんが玉を1個取り出し,取り出した玉を袋の中に戻した後,Bさんが玉を1個取り出す。2人が取り出した玉に書かれた数字の和が7以下となる確率を求めなさい。
４	桐光学園高校　（Ｒ６年）　★★★	８	三重県立高校　（Ｒ６年）　★★★
袋の中に,赤玉4個,白玉3個,黒玉1個の合計8個の玉が入っている。A,B,Cの3人がこの順番に袋から玉を1個ずつ取り出すとき,次の確率を求めなさい。ただし,取り出した玉は袋に戻さないものとする。 (1) 3人とも赤玉を取り出す確率 (2) Bが2個目の白玉を取り出す確率 (3) 3人が玉を取り出したあとに袋の中に3色すべての色の玉が残っている確率 1/14　　3/28　　17/28		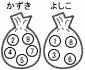1から9までの整数が1つずつ書かれた9個の袋があり,かずきさんの袋とよしこさんの袋にそれぞれいくつか入れる。かずきさんとよしこさんは,それぞれ自分の袋から1個の玉を取り出し,その取り出した玉に書かれた数が大きい方を勝ちとするゲームをしている。 　右の図のように,かずきさんの袋に2,4,5,7,9の数が書かれた玉を,よしこさんの袋に1,3,6,8,の数が書かれた玉を入れたとき, (1) このゲームで,かずきさんが勝つ確率を求めなさい。 (2) かずきさんの袋の2,4,5,7,9の数が書かれたいずれか１個の玉を取り出し,その玉をよしこさんの袋に入れ,ゲームをしたところ,かずきさんが勝つ確率と,よしこさんが勝つ確率が等しくなった。このとき,かずきさんの袋の2,4,5,7,9のいずれの玉を,よしこさんの袋に入れたか,その玉に書かれた数を答えなさい。

［TOP］［BACK］［NEXT］［解答］　　★中 ★★やや難 ★★★難　 印刷用